 |
|
Seminars 2010
Seminarios del Instituto Gregorio Millán
Jueves 9 de diciembre de 2010
Extraordinary optical transmission from a microwave
engineering perspective
Universidad de Sevilla
Abstract
Extraordinary transmission of electromagnetic radiation
through tiny holes (meaningfully smaller than the
wavelength of the involved radiation) made in opaque
metal screens was reported 12 years ago in the optical
regime. The phenomenon was soon explained in terms of
the interaction of the planar uniform impinging waves
with surface plasmon polaritons (SPP's) excited at both
sides of the metal screen. In a first stage the
phenomenon was thought to be characteristic of the
optical regime, since only at optical frequencies
metals support that kind of waves. However it was
theoretically and experimentally verified that the
phenomenon also happens at other frequency ranges after
proper scaling of the linear dimensions of the system.
Although the terminology extraordinary transmission has
been used for several diferent situations, the most
relevant case corresponds to the frequency selective
enhanced transmissivitty through periodic arrays of
subwavelength holes or slits. The speakers have
considered this case using the point of view of
microwave engineers, which is used to deal with
generalized transmission systems with discontinuities.
The use of the classical theory of waveguides leads to
simple models which are surprisingly accurate both from
the qualitative and quantitative perspectives. The talk
will illustrate how this approach explains the
essential physics behind extraordinary transmission and
provides a useful tool to design practical devices
based on this phenomenon. A review of published and
unpublished results will be presented to the audience.
![[Pdf file]](Css/pdf.gif)
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Seminarios del Instituto Gregorio Millán
Jueves 2 de diciembre de 2010
The hanging thin rod: A singularly perturbed eigenvalue
problem
UC3M
Abstract
We study the vibrations of a hanging thin flexible rod,
in which the dominant restoring force in most of the
domain is tension due to the weight of the rod, while
bending elasticity plays a small but non-negligible
role. We consider a linearized description, which we
may reduce to an eigenvalue problem. We solve the
resulting singularly perturbed problem asymptotically
up to the first modification of the eigenvalue. On the
way, we illustrate several important problem-solving
techniques: modeling, nondimensionalization, scaling,
and especially use of asymptotic series. ![[Pdf file]](Css/pdf.gif)
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Seminarios del Instituto Gregorio Millán
Jueves 18 de noviembre de 2010
Steepest-decent method for integrable systems (Part 2
of 2)
Duke University
Abstract
We examine integrable nonlinear systems, in particular
KdV (the Korteweg-de Vries equation) and NLS (the
focusing nonlinear Schrödinger equation). The equations
display their dispersive character particularly well in
a scaling of small dispersion often referred to as the
semiclassical scaling. The initial profile breaks into
fully nonlinear modulated oscillations that are often
multi-phase. We will describe recent methods for
solving the initial value problem in this scaling,
using rigorous asymptotics. Conceptually, the process
is analogous to linear PDE, where one can derive the
geometrical optics approximation by applying the
steepest descent method to the calculation of the
integral that expresses the field. In the nonlinear
case the object on which steepest descent is applied is
not an integral. It is a Riemann-Hilbert problem that
relates to the scattering theory of a linear operator.
This operator is associated to the nonlinear problem
and effects the solution of the nonlinear problem. We
will start with numerical results on the emergence of
oscillations and we will give an outline of the basic
ideas behind the the method of solution of integrable
systems and of the asymptotic calculation. ![[Pdf file]](Css/pdf.gif) Extended abstract: ![[Pdf file]](Css/pdf.gif)
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Seminarios del Instituto Gregorio Millán
Viernes 12 de noviembre de 2010
Steepest-decent method for integrable systems (Part 1
of 2)
Duke University
Abstract
We examine integrable nonlinear systems, in particular
KdV (the Korteweg-de Vries equation) and NLS (the
focusing nonlinear Schrödinger equation). The equations
display their dispersive character particularly well in
a scaling of small dispersion often referred to as the
semiclassical scaling. The initial profile breaks into
fully nonlinear modulated oscillations that are often
multi-phase. We will describe recent methods for
solving the initial value problem in this scaling,
using rigorous asymptotics. Conceptually, the process
is analogous to linear PDE, where one can derive the
geometrical optics approximation by applying the
steepest descent method to the calculation of the
integral that expresses the field. In the nonlinear
case the object on which steepest descent is applied is
not an integral. It is a Riemann-Hilbert problem that
relates to the scattering theory of a linear operator.
This operator is associated to the nonlinear problem
and effects the solution of the nonlinear problem. We
will start with numerical results on the emergence of
oscillations and we will give an outline of the basic
ideas behind the the method of solution of integrable
systems and of the asymptotic calculation. ![[Pdf file]](Css/pdf.gif) Extended abstract: ![[Pdf file]](Css/pdf.gif)
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Seminarios del Instituto Gregorio Millán
Jueves 28 de octubre de 2010
Convergent Power Series for Waves in Periodic
Metamaterials
Louisiana State University
Abstract
Fields in sub-wavelength periodic composite materials
are typically expanded in formal power series, with the
variable of expansion being the ratio of cell size to
wavelength. These series are typically only formal, or,
at best, asymptotic. But for Bloch waves in infinite
periodic media with high contrast, we prove that they
are actually convergent. We foresee utilizing the
method of convergent power series as a rigorous
framework for the analysis of the role of higher-order
multipoles in the creation of certain curious bulk
properties of metamaterials that have been observed in
numerical simulations. To this end, one must obtain a
quantitative lower bound on the radius of convergence
of the series, and this presents one of the major
challenges. I will begin by describing foundational
work of H. Schwarz, in which he used convergent power
series to devise the first general proof of the
existence of a Dirichlet eigenvalue, and then point out
the difficulties presented in the context of
metamaterials.
Joint work with R. Lipton and S. Fortes, Department
of Mathematics, Louisiana State University, USA.
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Seminarios del Instituto Gregorio Millán
Miércoles 26 de mayo de 2010
A new perspective on the moment closure problem in
radiative transfer
Temple University
Abstract
Radiative transfer can be modeled by a kinetic equation
that describes the evolution of the particle intensity
function in a high dimensional phase space of (at
least) time, position, and angle of flight. While a
direct simulation of the mesoscopic kinetic equation is
possible, many computational scientists prefer a
description by macroscopic equations. An expansion in
the angular variable yields an equivalent system of
infinitely many macroscopic moment equations. The
fundamental question how to best truncate this system
is the moment closure problem. Various closure
strategies exist. These are typically based on an
asymptotic analysis or assume higher moments be
quasi-stationary.
We present an alternative approach to derive moment
closures, based on the Mori-Zwanzig formalism of
irreversible statistical mechanics. The influence of
the truncated moments on the revolved moments is
modeled by a memory term. Suitable approximations to
this memory term allow us to re-derive existing
closures, such as PN, SPN, and diffusion correction
closures. In addition, new closures can be derived. We
propose a crescendo-diffusion closure, which improves
classical diffusion closures at no extra cost, as well
as a new class of parabolic-type closures.
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Seminarios del Instituto Gregorio Millán
Miércoles 28 de abril de 2010
Simulation of sedimentary patterns (dunes): emergence
of dune fields and dune stabilization driven by
vegetation growth
Laboratoire de Physique et Mécanique des Milieux
Hétérogènes, ESPCI
Abstract
Much alike sea waves, dunes are formed at desert
surfaces by the action of the wind. The existence of a
minimal size for Aeolian dunes of about 10m long, and
thus, the impossibility of generate them in wind tunnel
experiments, has led to a strong emphasis in numerical
simulations as the simplest, and sometimes the only,
tool to get insight into the dune emergence and
evolution under controlled conditions. In this talk,
I'll focus on two main applications of dune modeling:
first, the emergence of dune fields under different
external conditions, as a result of the coupling of
longitudinal and transversal instabilities; and second,
the inactivation of fully developed dunes. In the
latter case, by including vegetation growth into the
model, we are able to obtain a transition from active
barchans to inactive parabolic dunes, and hence, to
uncover the mechanisms underlying dune desactivation.
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Seminarios del Instituto Gregorio Millán
Miércoles 7 de abril de 2010
Mathematical modeling of rate independent hysteresis
and criticality in martensites
École Polytechnique
Abstract
We show that singular dissipative potential describing
rate-independent plasticity in shape memory alloys can
be obtained by homogenization of a micro-model with
quadratic (viscous) dissipation. The essential
ingredient making this reduction possible is a rugged
energy landscape at the micro-scale, generating under
external loading a regular cascade of subcritical
bifurcations. The rate-independent plastic deformation
emerges in this description as a continuous succession
of infinitesimal viscous events; the limiting procedure
presumes the elimination of small time and length
scales. Our prototypical model reproduces most of the
experimental observations in martensites including self
organization to criticality and power law acoustic
emission. Criticality is currently attracting a great
deal of interest due to its ubiquity in nature from
turbulence to earthquakes. Our explanation of the
emergence of criticality in martensites is based on the
idea that the disorder needed for criticality is not
quenched but is acquired by the system in the process
of cyclic deformation. ![[Pdf file]](Css/pdf.gif)
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Seminarios del Instituto Gregorio Millán
Lunes 22 de marzo de 2010
Multi-level Optical Imaging Algorithm Based on
Radiative Transport Equation
UC Irvine
Abstract
In this talk I will first discuss a fast forward solver
for radiative transport equation (RTE), the most
accurate model for in vivo photon migration which is
crucial for optical and molecular imaging. Our
algorithm is based on a novel multigrid method in both
physical and angular space that can effectively deal
with different regimes of transport. Then I will
introduce a few a multi-level optical imaging
algorithms that can achieve high resolution with
reduced computation cost and improved stability. Based
on noise model and prior information we propose various
combinations of fidelity and regularization. Our recently developed fast multigrid RTE solver and imaging methods are available at http://sites.google.com/site/rtefastsolver. ![[Pdf file]](Css/pdf.gif)
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Seminarios del Instituto Gregorio Millán
Miércoles 24 de febrero de 2010
Aerosol coagulation: General theory, mathematical
methods and recent extensions for coagulation in
expanding gases
UNED
Abstract
The coagulation rate of a suspension of particles in a
carrier gas is well explained by Smoluchowski's theory,
which considers the diffusion of particles as the
physical process that determines this rate, leading to
the well known Smoluchowski's coagulation kernel.
Once the coagulation rate is known, the evolution equation that determines the PDF of the aerosol (particle number density in terms of particle volume) is a non-linear integro-differential equation, which in general is difficult to solve. One of the reasons for this, is because, with the usual coagulation rates, the "region of interest" (where the PDF is mainly located) grows very fast with time, which, on the other hand, produces a very fast decrease with time of the numerical accuracy of any given discretization. As a consequence, a very fine discretization is needed if one wants to have high numerical accuracy throughout the whole process. This makes this problem very time consuming, especially because one is usually interested in computing the evolution of the initial PDF until the self-preserving PDF is attained, which in many cases happens at long times. A mathematical method to deal with this problem will be introduced in the first part of the talk. While several generalizations of Smoluchowski's
theory have been known for some time, the influence of
density variations of the carrier gas in the
coagulation rate has not been considered before. A
recent extension of Smoluchowski's theory that includes
this effect will be the topic of the second part of the
talk.
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Lectura de Proyecto de Tesis Doctoral
Martes 23 de febrero de 2010
Estudio de modelos discretos de nucleación y formación
de biopelículas
FCT/UNL
La lectura tendrá lugar a las 12:00 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Seminarios del Instituto Gregorio Millán
Jueves 18 de febrero de 2010
Some wonderful conjectures (but almost no theorems) at
the boundary between analysis, combinatorics and
probability.
New York University/University College London
Abstract
The function $$F(x,y) = \sum\limits_{n\ge 0}
\frac{x^n}{n!} y^{n(n-1)/2}$$ arises in statistical
mechanics as the generating function of a single-site
lattice gas, and in numerous problems in combinatorics,
notably in the enumeration of connected graphs. It is
in some ways the simplest entire function after the
exponential function, to which it reduces when $y=1$.
Nevertheless, it has been surprisingly little studied.
I will present here some amazing conjectures concerning
the roots $x_k(y)$ of $F(x,y)$, discovered empirically
with a little help from Mathematica. This talk is
intended to be understandable to mathematicians,
applied mathematicians and physicists from a wide
variety of backgrounds. ![[Pdf file]](Css/pdf.gif)
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
Seminarios del Instituto Gregorio Millán
Miércoles 17 de febrero de 2010
Finite-length effects in Taylor-Couette flow
Duke University
Abstract
The term Taylor-Couette flow refers to fluid flow
between rotating concentric cylinders. The onset of
cellular motion in such flow (in particular, the
remarkable agreement Taylor obtained between experiment
and a theoretical stability analysis) played a central
role in the history of fluid mechanics. More recently,
this excellent agreement has come to seem confusing, in
light of attempts to reconcile the fact that
experiments are performed in an apparatus of finite
length while Taylor's analysis considered an infinite
apparatus. In an infinite apparatus, steady flows with
secondary circulation in cells bifurcate from the
trivial solution when the Reynolds number Re exceeds a
critical value Re${}_c$. Because of translational
invariance, the bifurcation is symmetric, as sketched
in Figure 1. Based on the feeling that in a long
apparatus end effects ought to be small, researchers
sought to understand experiments as a slightly
perturbed bifurcation, such as sketched in Figure 2.
Thus, in an experiment in a finite-length apparatus,
the onset of cells is smeared out, compared to the
abrupt onset in Figure 1, and only one of the two
solution branches (the so-called normal modes) can
evolve if the rotation speed is increased
quasi-statically from rest. However, provided the
apparatus is long, then one also expects that
![[Pdf file]](Css/pdf.gif) 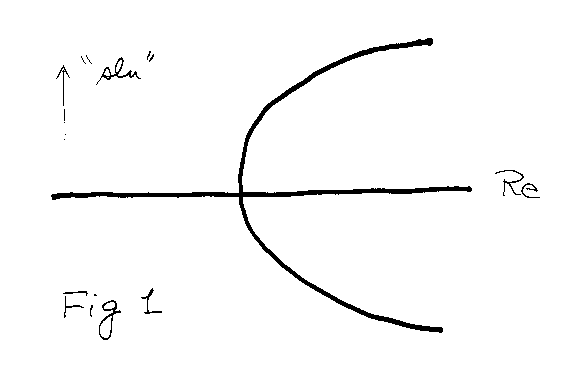 
El Seminario tendrá lugar a las 12:30 horas en la Sala
2.1.D04 (Edificio Sabatini) Universidad Carlos III
|
|
|
Last update on 27/August/2025 by
Webmaster (
) |
|